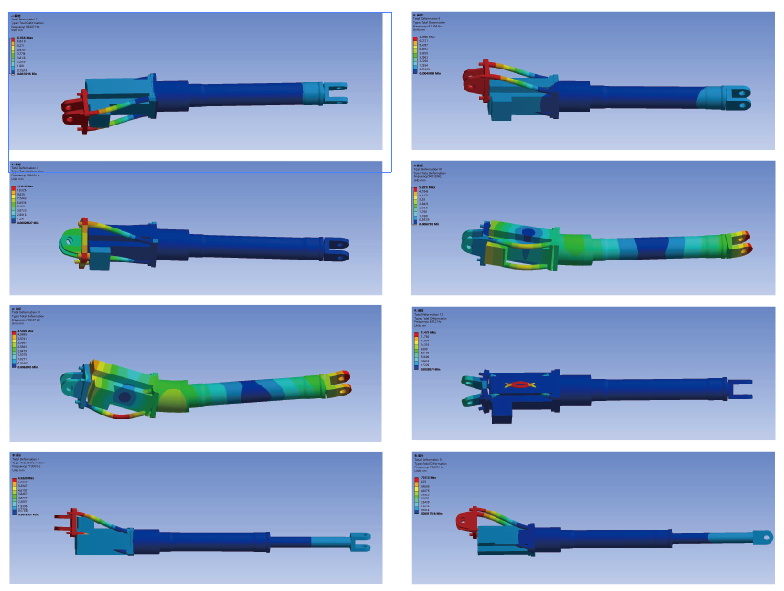
The basic idea of the finite element method is: through the node displacement of the element, the displacement field of the entire element can be obtained by using the interpolation function. Next is the derivation of the element stiffness matrix and load vector. According to the assumed displacement function, the element stiffness matrix [K]e and load vector {p}e can be derived by using equilibrium conditions and the principle of minimum potential energy. Afterwards, the unit stiffness matrix is assembled to obtain the total stiffness matrix of the structure, and the overall balance equation of the structure is obtained: [K]{δ}=[P], where [K] is the total stiffness matrix, and {δ} is the overall structure Node displacement, [P] is the external force acting on the FE nodes of the entire structure. Finally, according to

The boundary conditions of the problem are solved to obtain a simplified equilibrium equation system, and the node displacement {δ} can be obtained through the simplified equilibrium equation system. According to the obtained node displacement, the unit strain and stress.

The design load of the structure is equal to the service load multiplied by the safety factor. When the ultimate bearing capacity of the structural material is greater than or equal to the design load of the structure, or when the ultimate stress of the structural material is greater than or equal to the stress caused by the structural design load, the structure is considered to be safe, which is the static strength design criterion,

Its expression is:

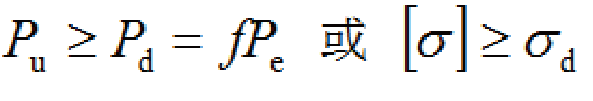
In the formula, Pu is the ultimate load, Pd is the design load, f is the safety factor, Pe is the service load, [σ] is the ultimate stress, and σd is the structural stress caused by the design load.