The physical meaning of amplitude-frequency characteristics and phase-frequency characteristics

Amplitude-frequency response explores the relationship between frequency and its amplitude. A signal usually contains many frequencies. When passing through a circuit, the gain (or attenuation) obtained by different frequencies is different. What needs to be discussed is how to avoid or reduce the effects caused by these inconsistencies. Impact. The phase-frequency response discusses the phase offset caused by different frequencies passing through a circuit. The so-called phase offset is actually a time delay. According to coswt, we know that the phase is a function of time, so it is more intuitive to directly understand it as a time delay.

So we give the system a sinusoidal input signal, and the system output response changes differently with the angular frequency w of the sinusoidal input signal. The variation pattern of the output amplitude with w is the amplitude-frequency characteristic, and the phase difference between the output phase angle and the output phase angle and the variation pattern of w constitute the phase-frequency characteristic.

The frequency characteristics of the platform refer to the impact on different frequency components of the signal passing through the platform. This impact is reflected in:

1. Amplify or reduce the amplitude of different frequency components of the input signal;

2. Cause phase deflection to components of different frequencies of the input signal. The first impact of the system on the input signal, with frequency f as the abscissa and the factor of amplifying or reducing the amplitude ratio as the ordinate, the two-dimensional curve is the amplitude-frequency response curve of the system, recorded as A(f ). In the same way, with the frequency f as the abscissa and the phase deflection as the ordinate, the curve drawn is the phase-frequency response curve of the system, recorded as a(f).

The amplitude-frequency response is relatively easy to understand. Any point A(f) on the curve indicates whether the system has enhanced or weakened a certain frequency component of the input signal. If it has weakened, by how much.

The phase-frequency response is more obscure to understand. Literally understood, any point a(f) on the phase-frequency curve represents the response of the system to a certain frequency component f of the input signal (that is, a sine wave oscillating at frequency f, according to

The phase of Fourier series expansion) is output after being rotated by a(f) radians, that is, the phase difference between the output signal and the input signal at a certain frequency f is a(f). In fact, for a sine wave, the deflection of the phase is equivalent to the wave propagating for an extra period of time, and how long it propagates depends on the frequency of the wave (a sine wave with a high frequency must deflect a certain phase for a shorter time than the frequency) There are fewer sine waves. That is to say, when deflected in the same phase, the higher the frequency, the shorter the delay). Therefore, the phase deflection of the system on the input signal is equivalent to a certain delay on the signal, and this delay may be different for different frequency components, and this is the physical meaning of the phase-frequency response.

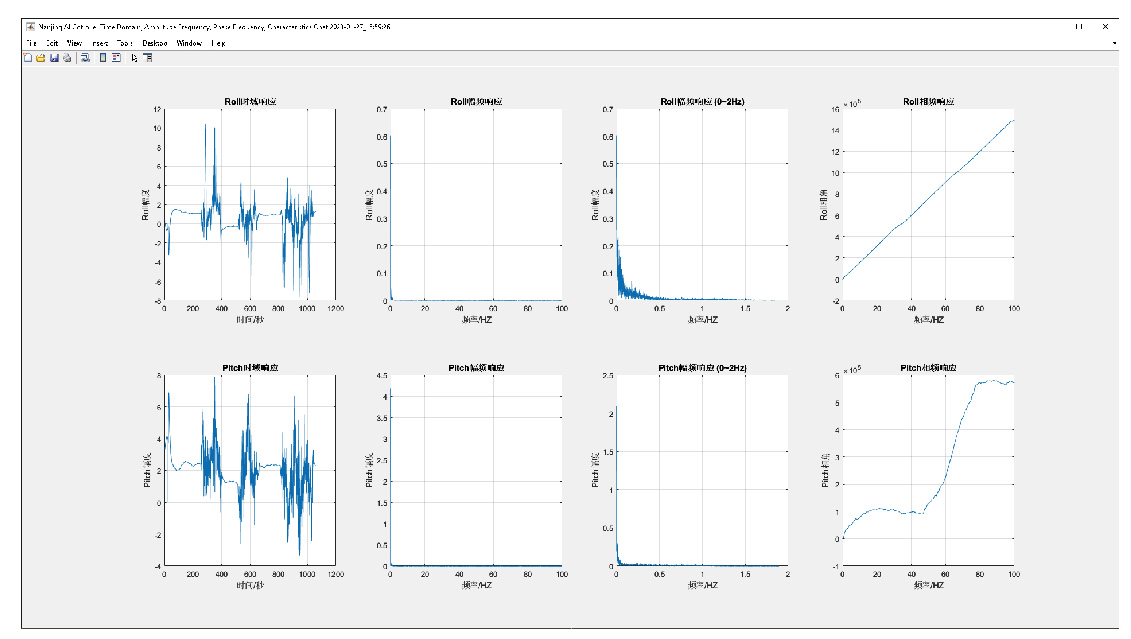
Road spectrum/flight spectrum/wave spectrum amplitude frequency phase frequency characteristic diagram

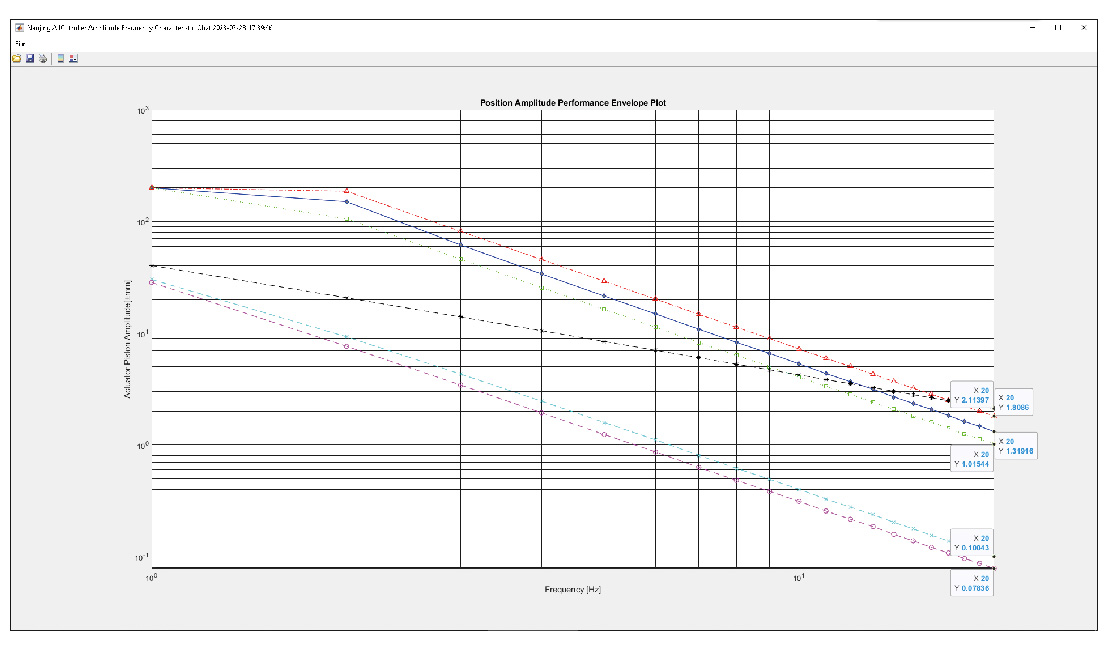
Amplitude-frequency characteristics diagram of the 6dof of the motion platform

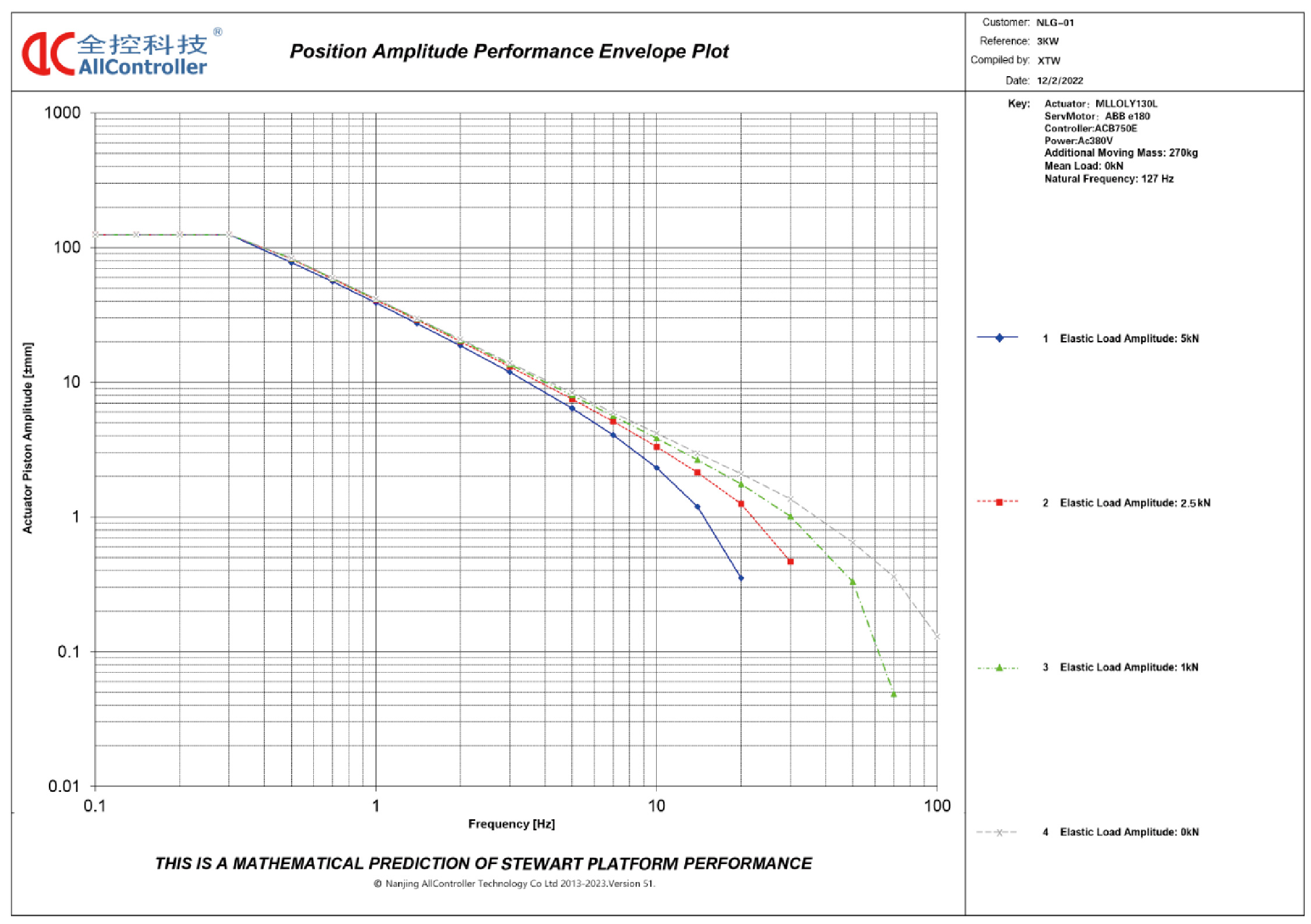
Motion platform position amplitude envelope diagram